[最も人気のある！] 比の式 作り方 125338-比の式 作り方

 比例の式を作りたければ、\(y=ax\)の形を覚えておいて、そこに\(x, y\)の値を代入するだけでOKですね。 比例の式グラフから式を作る 次の関数の式を作りなさい。 決算書の「対売上比」を表示したい、 という場面が結構あります。 ※対売上比＝各科目の金額÷売上高 この場合、 全ての科目について「分母は売上高」 →式をコピーしても、分母は売上高で「変わらないでほしい」 という状況ですので、 式をコピーしても参照先セルが変わらない 絶対参照が役に立つわけです。 証明 \displaystyle \frac {a b} {a − b} = \frac {c d} {c − d} (＊) \left\ {\begin {array} {l} a = bk \text {①}\\ c = dk \text {②}\end {array}\right \displaystyle \frac {c d} {c − d} = \frac {dk d} {dk − d} = \frac {d (k 1)} {d (k − 1)} = \frac {k 1} {k − 1}

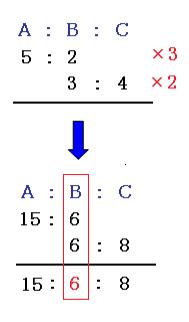
比の性質を解説 比例式や連比の解き方だってこんなに簡単

比の式 作り方

25 ++ 割合 求め 方 小学生 323660-割合 求め方 小学生

割合の問題を苦手にしている生徒さんは多いです。 しかし、ポイントは2つです。 1どの割合の問題が上記で扱った割合の3パターンのどの問題にあてはまるか判断する 2判断したら、その3パターンの割合の問題を数式に表し、下記にあげた3パターンで解く。 以上、『簡単な 割合 の求め方『くもわ』の法則』の無料学習プリントを紹介しました。 速さ・時間・距離を表す「はじきの法則」の法則によく似た『くもわの法則』ですがはじきの法則と同様に簡単に公式を覚えることができます。 この図を見て公式を覚えたら問題ををたくさん解いて割合割合の3 用法 † 割合= くらべる量¥もとにする量 † くらべる量= もとにする量£割合 † もとにする量= くらべる量¥割合 どのテキストも大体こんな調子です。そして問 題に入ると、 問1 たてが15cm、横が9cm の長方形があります。 横に対するたての割合を求め

小5 算数 割合 解説動画 Youtube

割合 求め方 小学生

[新しいコレクション] 割る数 割られる数 覚え方 645641-割る数 割られる数 覚え方

 割られる数と割る数の頭の数字 を比べて、 割る数よりも割られる数が大きい場合には 割られる数の桁数－割る数の桁数 1桁 ＝商の桁数 になります 割られる数？割る数？何だか分かりにくいので、 左デカ！！ と覚えちゃいましょう 分子は割られる数で、分母は割る数と同じ意味なのです。 つまり、割り算と分数の関係をイラストであらわすと、次のようになります。 割り算記号の左を分数の上の段に、割り算記号の右を分数の下の段にもってくる と覚えてOKです。 わり算は数がどんなに大きくなっても小さくなっても、 割る数と割られる数の割合が変わらなければ、 答えは同じです。 端数のない大きな数、例に挙げておられる45万であれば45、 561万も561にして計算すれば答えは同じです。

分数 の英語 3 13などの読み方と正しく伝わる簡単テクニック

割る数 割られる数 覚え方

√1000以上 ピストン 作り方 522518-ピストン 作り方 モ��ター

テクニック ピストン Minecraft Japan Wiki

 マイクラ（マインクラフト）攻略班 最終更新日： 1752 ︎Twitterアカウント開設しました ︎最新アップデート情報 ︎コマンド一覧 ︎トラップ一覧の簡単な作り方 ︎簡単に作れるおすすめの自動装置一覧 マイクラにおける、ピストンの基本情報を掲載しています。 ピストンの入手方法や使い方までをまとめているので、ピストンについて知りたい 👉3×2 キャッスル・ゲートの作り方～ノスクラ（546） 森の踏切番日記 👉 👉 あと少しで出来そうなんですけどね そこで今回は、もう少し粘ってみようと思います。まず、レバーの位置を変

ピストン 作り方 モーター

選択した画像 立方体 体積 145528-立方体 体積 計算

Pref Chiba Lg Jp

立方体 体積 計算

表 単位 どこ 343529-表 単位 どこ

3

表 表にすると下記のようになります。 表1 18年店舗別月間来客数 表で数値を確認すると、a店の来客数合計がほかの2店より多いことや、8月の来客数は2月の約2倍だということが分かります。 印刷の現場でよく使われる「級」 印刷・DTPの現場では、ポイントではなく「級」という単位が使われることがよくあります。 どれくらいの大きさなのかというと、025 mmになります。 この「級」という単位は、1 Q、2 Qといったようにアルファベットを使って表記されます。

表 単位 どこ

[コンプリート！] 億の上 単位 911638-億の上 単位

製品別売上 単位：億円,% 12 区 分 増減 増減率 増減率 金額 構成比 金額 構成比 ﾊ ﾟ ﾜ ﾄ ﾚ ｲ ﾝ 11,7 356 12,044 357 256 21 71 熱 10,015 302 10,608 315 593 56 55 情報安全 5,454 165 5,031 149 423 84 163最終更新日16年7月16日 ー音訳の部屋へ戻るー 始めに 単位の読み方辞典（1）ではsi単位について記載しました。 単位の読み方辞典（2）では実際に使用する単位一覧を記載します。 単位一覧は物象の状態の量・呼び名・単位記号（単位の略字）・補助計量単位（10の整数乗単位）を記しました。3年間合計で1,050億円を計画。 機能材料セグメントを中心に、成長戦略に3年間で550億円を投じる 300 50 80 60 60 100 400 （単位：億円） 主な成長設備投資内訳 1,050 設備維持更新 成長戦略5 安全 環境 50 機能材料 金属 自動車 部品 ・mlcc用銅粉 ・ ・四輪向け触媒

2

億の上 単位

√完了しました！ 顎 キャ���クター 100013-顎 キャラク���ー

Web顎（あご、頷、英 jaw ）は、それを持つ動物一般においては、口の一部であって、開閉して物を捕らえる機能を有する構造体を指す。 ヒトを含む顎口上綱の動物では、頭の下部にあってWeb キャラクターストリートもなかなかの混み具合でしたし、ラーメン屋さんも行列が出来ていました 😊 屋内でもノーマスクの方や顎マスクの方が以前とは違いチラホラ。 大丸Web鼻の下と顎に髭のあるキャラであれば、「まじかる無双天使 突き刺せ!!呂布子ちゃん」の夏侯惇というキャラでしょうか。 非常にマイナーなジャンルで申し訳ありません。 顎だけならaph

アゴが100cm伸びる 史上最高のキャラ 香取ファミ平 誕生 ファミペイtvcm 香取ファミ平さま御来店 篇特別映像 解禁 新しい地図

顎 キャラクター